理解条件概率
样本空间(Ω)
样本空间通常指实验或随机所有可能的集合,我们常在说一个概率的时候,实际上是默认忽略掉了样本空间,比如说事件A的概率,实际上指样本空间中,事件A的数量与样本空间的占比。

比如丢硬币,硬币只有正面和反面,那么硬币的样本空间则为:
$$ \displaystyle \{正面,反面\} $$
这个时候常说的正面的概率为二分之一,实际指的是正面事件的数量与样本空间的占比,也就是$ \frac{1}{2} $。 再比如说丢骰子,一个骰子有6种可能,分别对应1-6不同的数值,那么丢骰子的样本空间则为:
$$ \displaystyle \{1,2,3,4,5,6\} $$
这个时候丢到5的事件概率则为数字5在样本空间出现的次数与样本空间总数的占比,为$ \frac{1}{6} $。
独立事件
独立事件是指不受过去已发生的事件而影响的事件,典型的例子就是抛硬币,不管你抛多少次硬币始终正面或反面的概率为0.5,而该硬币的样本空间如下:

独立事件的概率计算公式为如下:
$$ \displaystyle 事件发生的概率(P)=事件在样本空间中的数量/样本空间的事件总数 $$
比如用抛硬币的例子,计算正面的概率则为:
$$ \displaystyle P(正面) = \frac{1}{2} $$
而除了单个独立事件,有些时候也会求多个独立事件的概率,而多个独立事件的概率则是每个独立事件发生的概率的积。 比如掷3次骰子都为6的概率是多少?需要注意因为掷骰子是一个独立事件,即每次掷的骰子样本空间都一样,并且没有因为第一次掷骰子的结果会影响到下一次。 骰子的样本空间为下,从中能够得到单次掷骰子为6的概率为1/6:

而这个时候只需要将三次掷骰子的概率相乘就得到了三次都为6的概率:
$$ \displaystyle P(3次6) = \frac{1}{6} * \frac{1}{6} * \frac{1}{6} = \frac{1}{216} $$
相关事件
相关事件和独立事件是相对的,相关事件的发生概率会受到过去已发生事件的影响,每个事件都和上一个事件有关联,这些事件便是相关的。 比如一个布袋中有5个球,其中包含2个蓝球,三个红球,布袋(样本空间)则为:
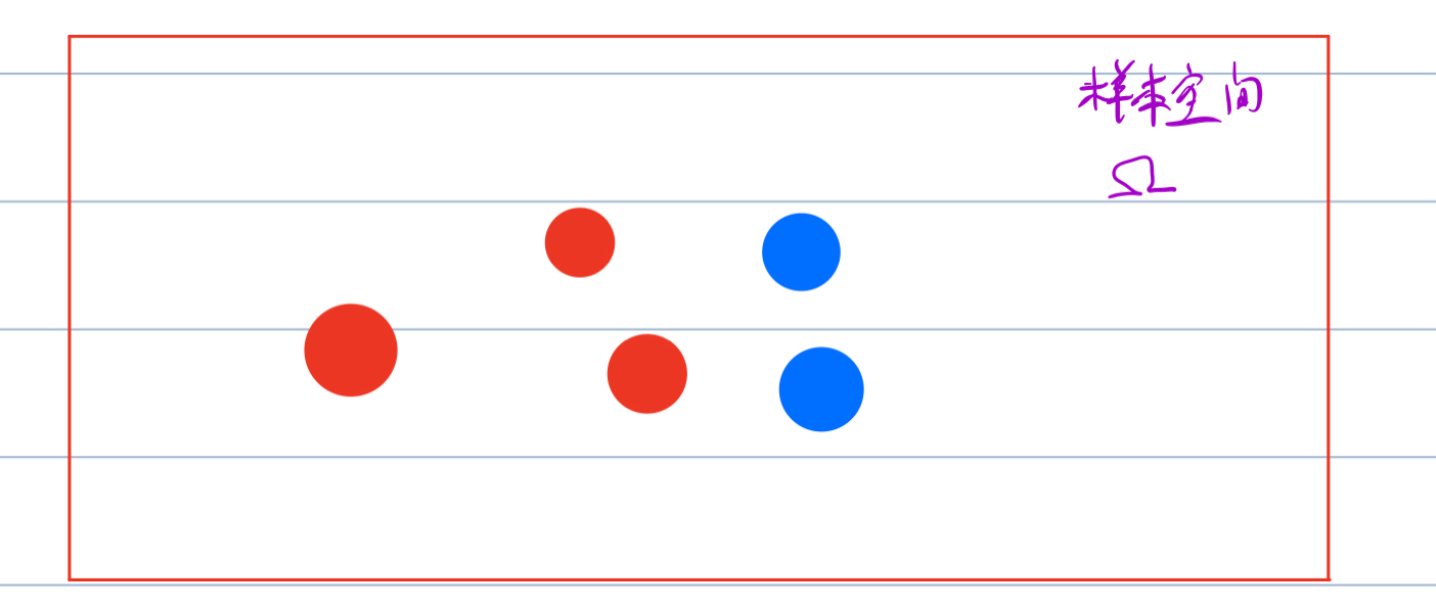
这个时候如果随机拿一颗蓝球的概率是多少?概率为2/5。 但是此时求第二次拿到蓝球的概率是多少?这个时候就会有两种情况发生:
- 第一次拿到红球,这个时候整个样本空间少了一个红球,所以第二次拿到蓝球的概率为2/4
- 第二次拿到蓝球,这个时候整个样本空间少了一个篮球,所以第二次拿到蓝球的概率为1/4
用图表示则为:
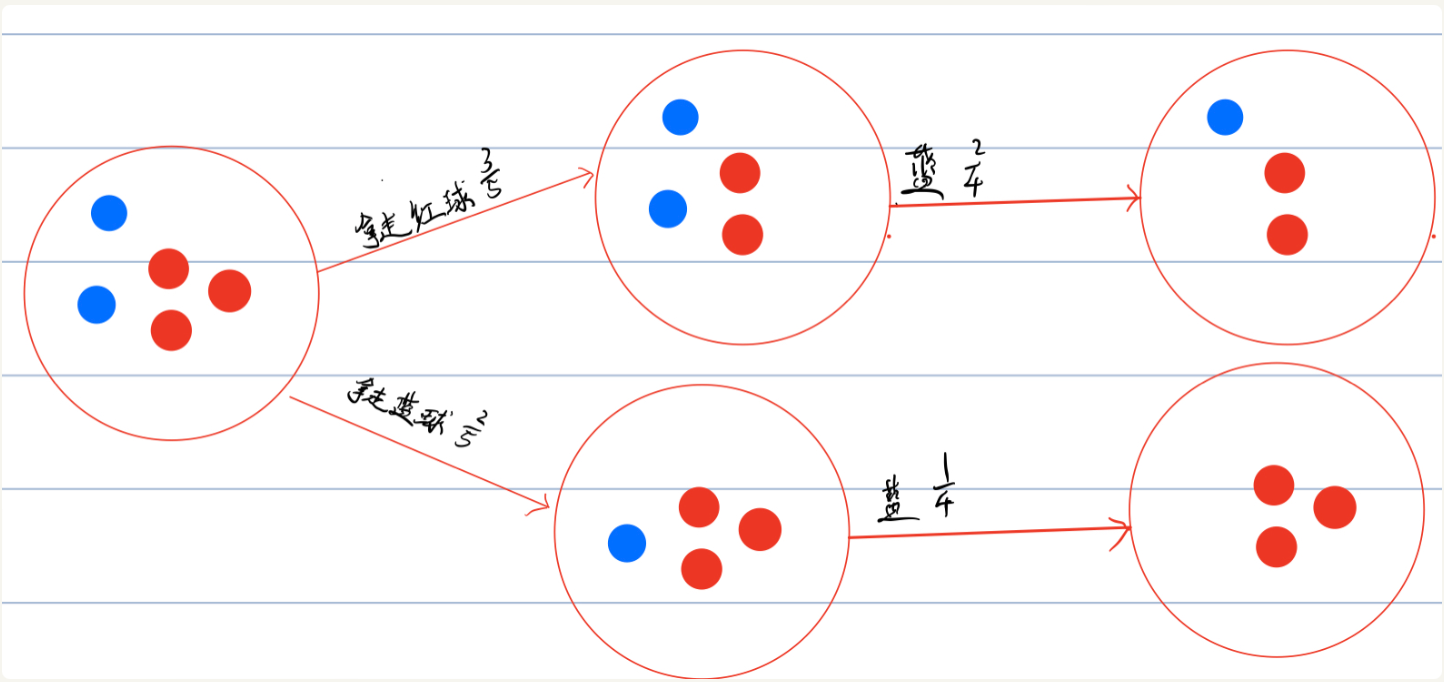
所以此时,如果算第一次拿到红球后,第二次拿到蓝球的概率则为:
$$ \displaystyle P(第二次拿到篮球) = \frac{3}{5} * \frac{2}{4} = 0.3 $$
如果算第一次拿到蓝球后,第二次拿到红球的概率则为:
$$ \displaystyle P(第二次拿到篮球) = \frac{3}{5} * \frac{1}{4} = 0.1 $$
条件概率
条件概率是研究相关事件的,指的是当B事件发生后,A事件发生的概率,用$ | $来表示”以下发生的条件下”,表示为公式:
$$ \displaystyle P(A|B) $$
比如上面的例子,第二个蓝球的概率是多少,这个问题就是条件概率,因为第二次抽中蓝球的概率是基于第一次拿了一颗球过后发生的事件。 这个时候可以将第一次抽中红球记作事件A,第二次抽蓝球为事件B,因为第二次抽球是在事件A发生的情况下而发生的,所以记作$P(B∣A)$ ,表示在A发生后,B发生的概率。 而这个概率可以根据下图来得到,即2/4:
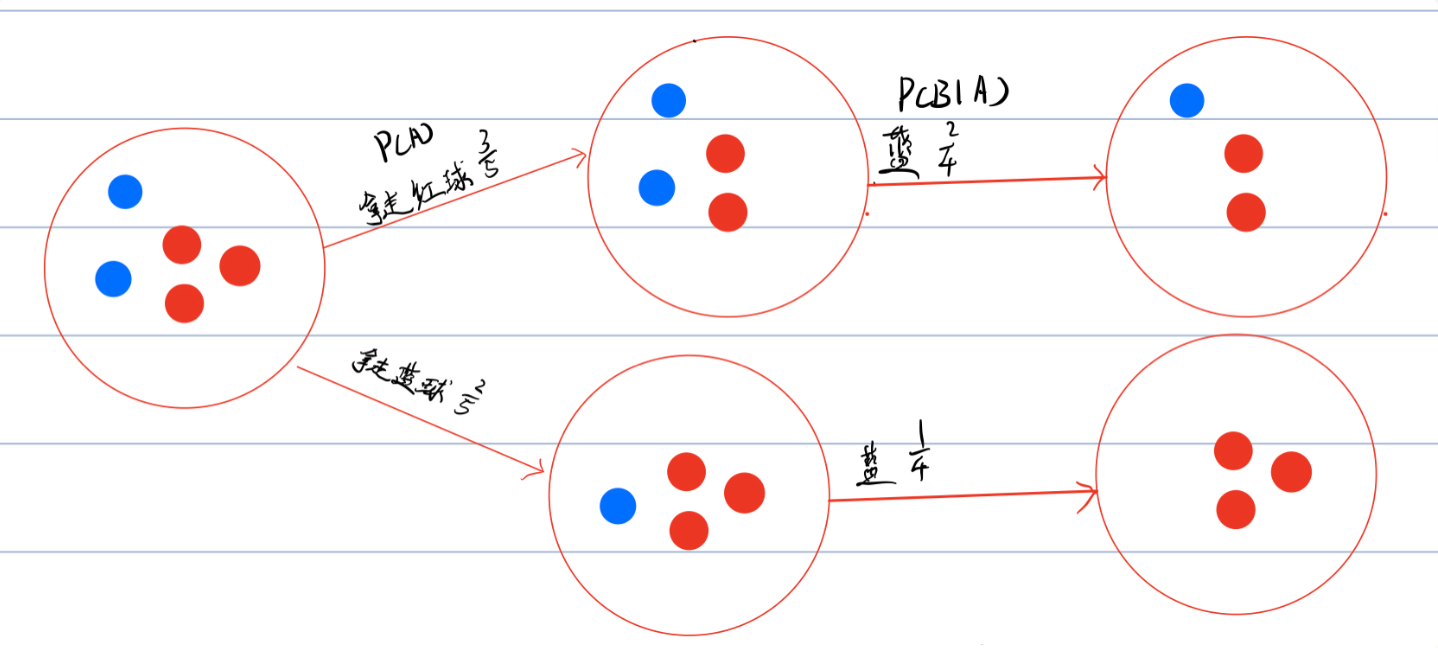
这里的条件概率本质是二级概率,该情况可以用图来表达,第一次抽球的样本空间为整个样本空间:
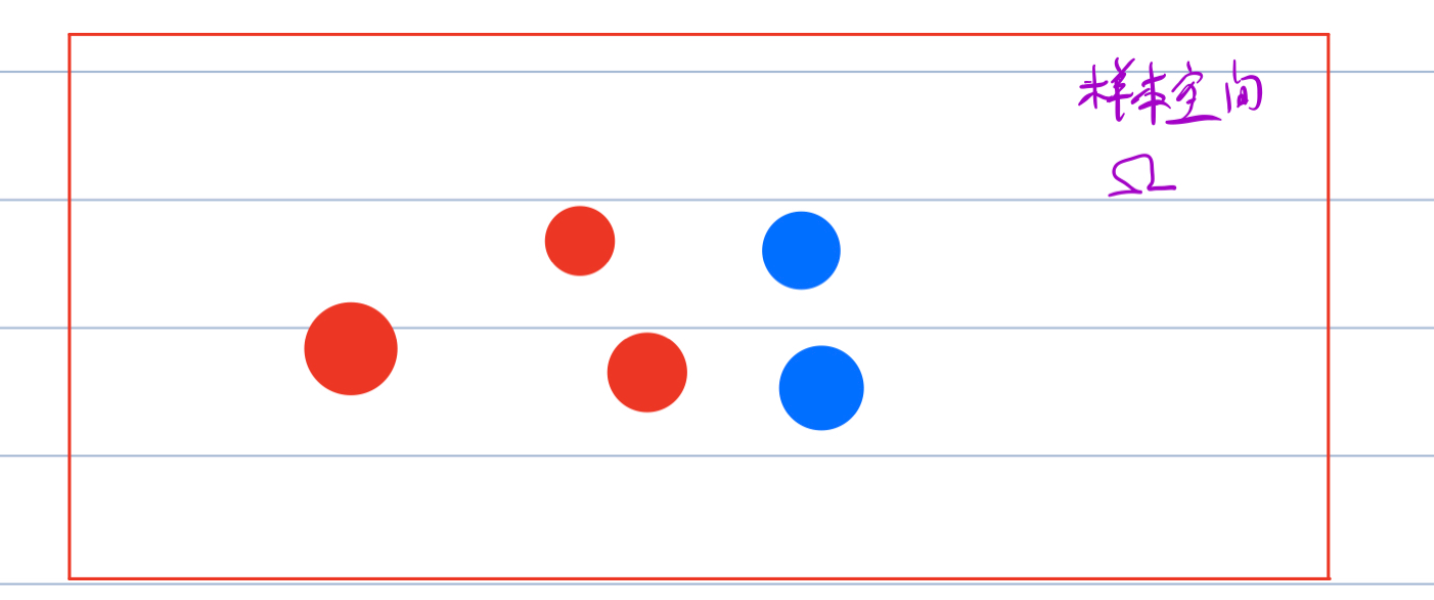
当第一次抽球(A事件)发生后,B事件的样本空间则是基于A事件发生后的样本空间,即下图中A圆圈内的样本空间:
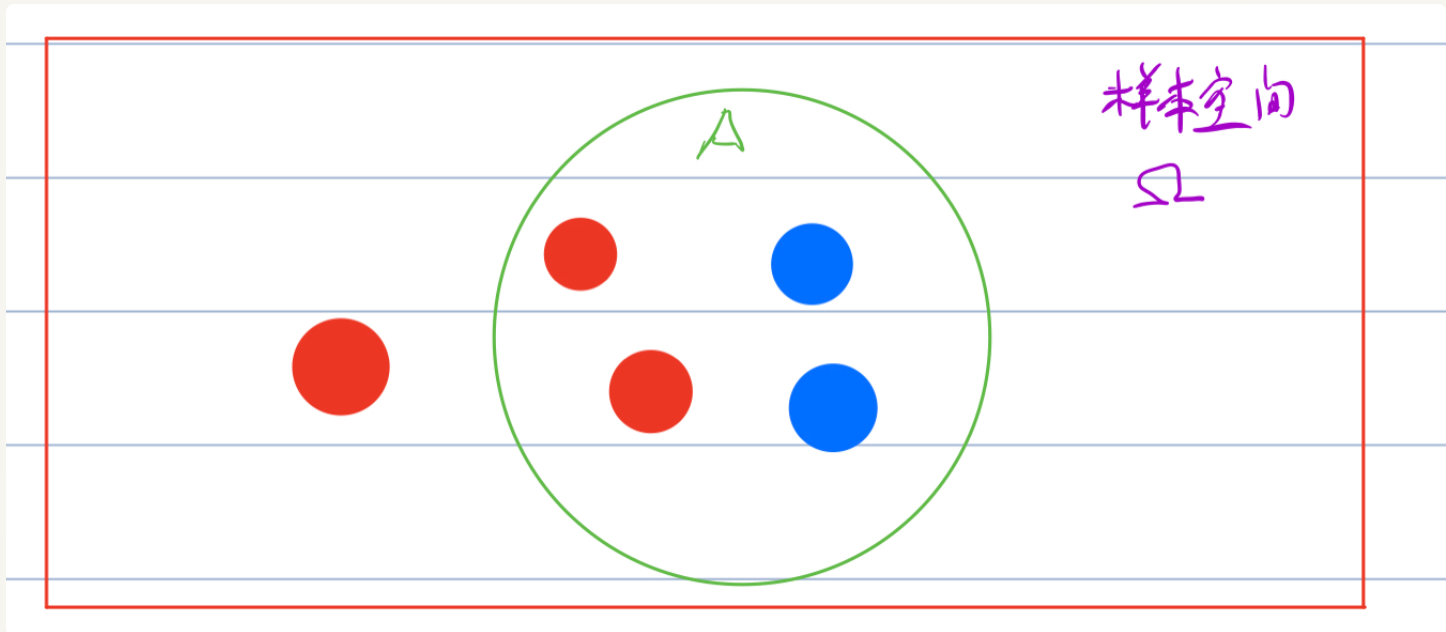
联合概率
联合概率指两个事件共同发生的概率,比如A和B事件共同发生的概率表示为:
$$ \displaystyle P(A,B) 或 P(AB) 或 P(A\cap B) $$
联合概率的计算分为两种情况,一种为独立事件,比如前面掷骰子,计算公式则为多个独立事件事件的积,表示为:
$$ \displaystyle P(A\cap B) = P(A) * P(B) $$
另一种则为相关事件,比如上面的抽球的例子,则可以通过反推来计算,表示为:
$$ \displaystyle P(A\cap B) = P(B|A) * P(A) $$
这里这样计算是因为P(B|A)只得到了B在A发生后的概率,也就是在发生后的样本空间上计算的,所以P(B|A)表示的只有下图这么一部分发生的概率:
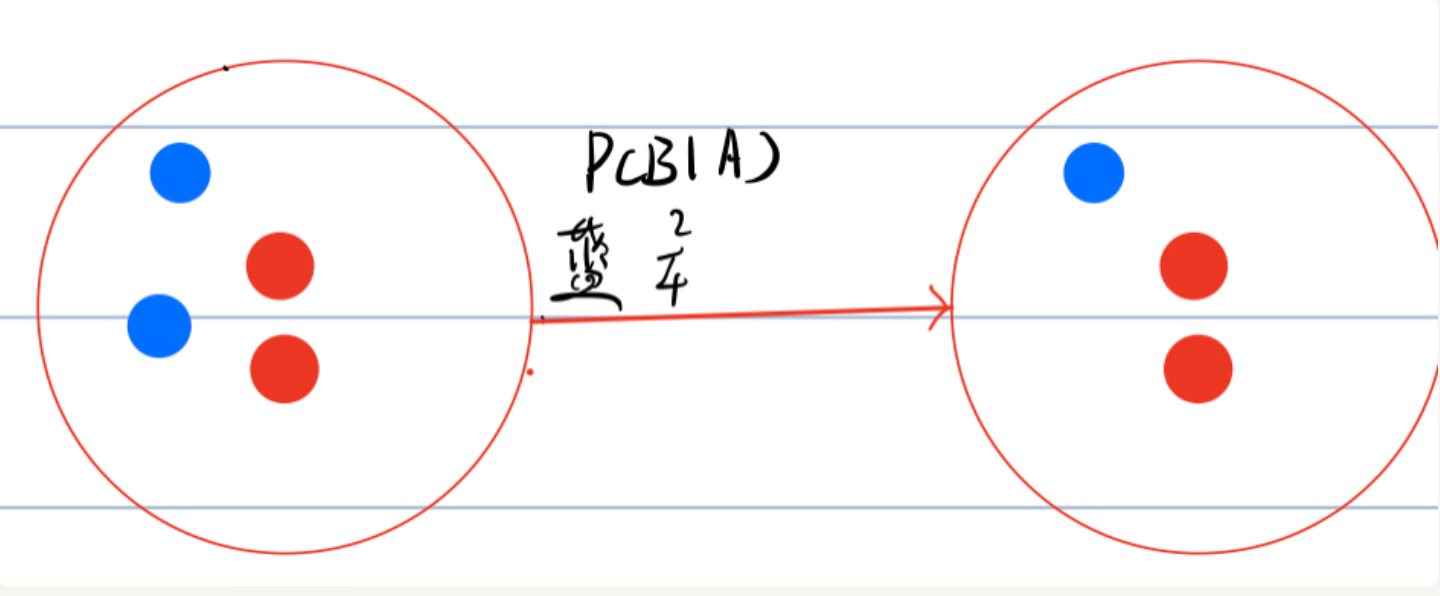
而在这个时候乘以P(A)的概率,则就能表示如下这整个部分:
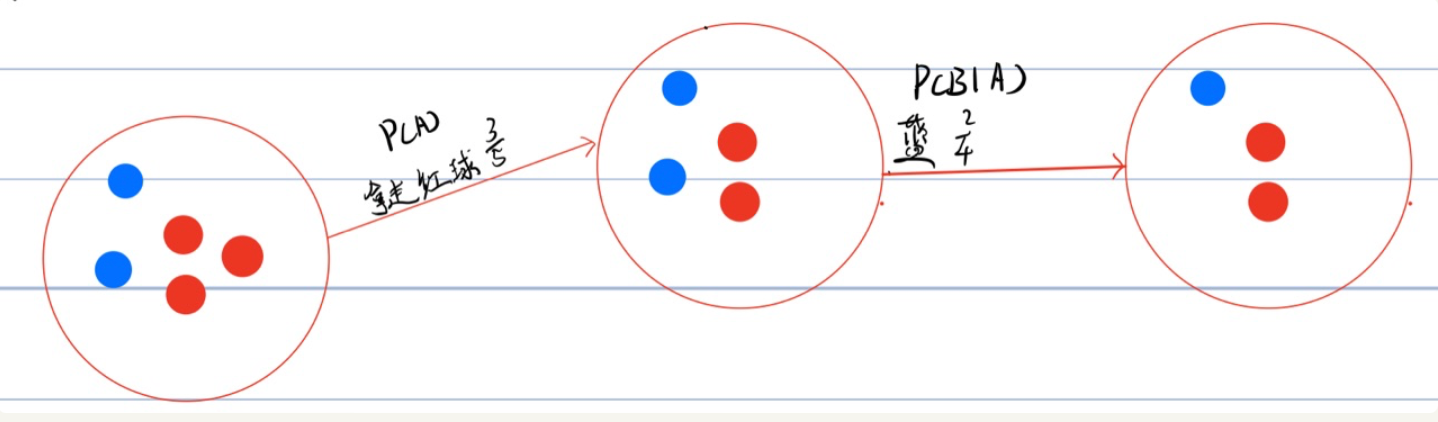
全概率
导致一个事件发生的原因有很多种,那么该事件发生的概率就是每种原因引起该事件发生的概率总和,这句话能够很好的解释全概率。 而全概率公式就可以计算出一个事件的全部概率,公式为:
$$ \displaystyle P(B) = \sum\nolimits_{n}^{i=1} P(B\cap A_i) $$
而根据联合概率的计算方法,可以写成下面这样:
$$ \displaystyle P(B) = \sum\nolimits_{n}^{i=1} P(B|A_i) * P(A_i) $$
还是拿红蓝球的例子来说,如果需要计算P(B),这个时候可以利用全概率公式,则将能引起事件B发生的每个概率相加,即可得到P(B)。 在红篮球例子当中,引起事件B的原因有两种,分别为:先拿到红球,然后抽中蓝球的概率和先拿到蓝球抽中蓝球的概率。 根据图中第一种先拿到了红球引起B事件的发生的概率为$ (3/5)∗(2/4)=0.3 $:
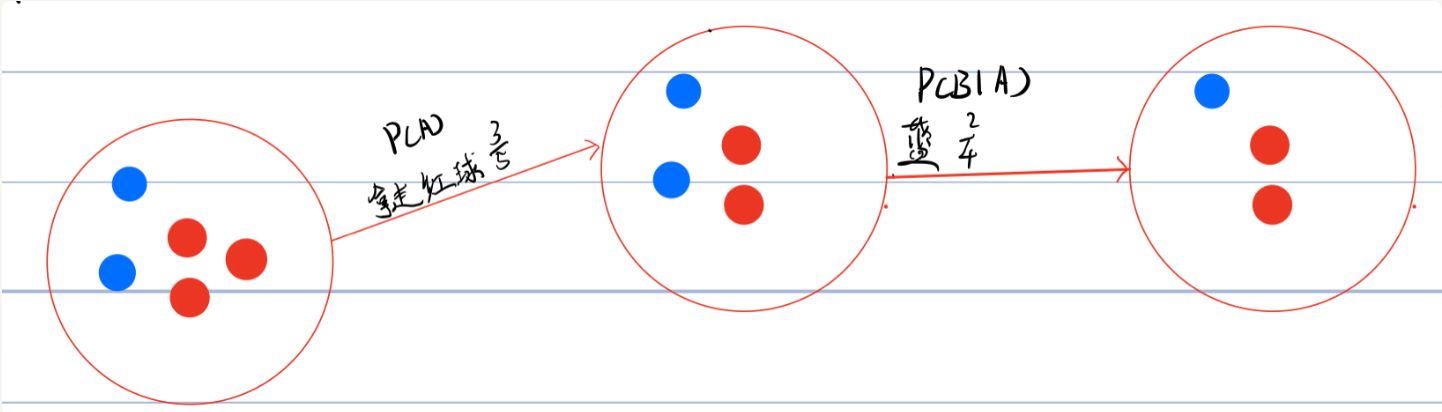
根据图中第二种先拿到了蓝球引起B事件的发生的概率为 $ (2/5)∗(1/4)=0.1 $:
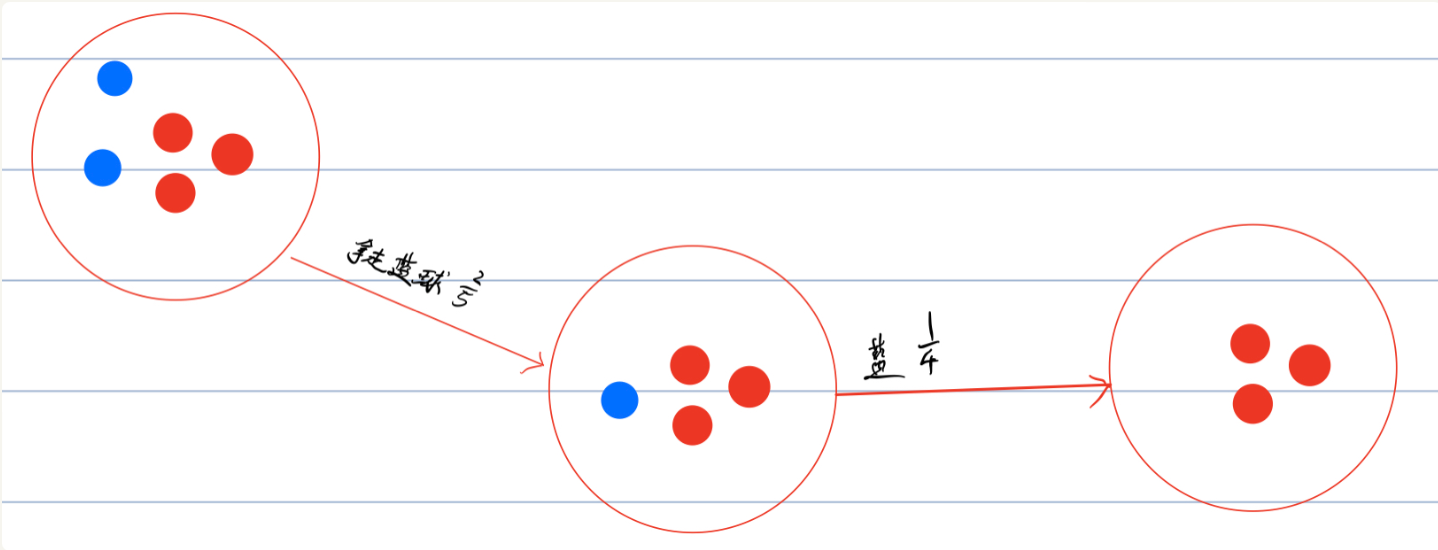
这个时候得到了所有能引起B事件发生的原因的概率,所以:
$$ \displaystyle P(B)=0.3+0.1=0.4 $$
条件概率和朴素贝叶斯定理公式
在理解了上面的几个知识点后,就能够理解贝叶斯和条件概率的计算方式。 条件概率的计算公式为:
$$ \displaystyle P(A|B) = \frac{P(A \cap B)}{P(B)} $$
而贝叶斯公式则可以用条件概率公式和联合概率公式推导出来:
$$ \begin{align} (1):P(A|B) = \frac{P(A \cap B)}{P(B)} \\ (2):P(A\cap B) = P(B|A) * P(A) \\ (3):P(A|B) = P(B|A) * P(A) / P(B) \end{align} $$参考文档
- https://zhuanlan.zhihu.com/p/134036707
- https://blog.csdn.net/u013371163/article/details/60469065
- https://www.shuxuele.com/data/probability-events-conditional.html
- https://www.shuxuele.com/data/probability-events-independent.html
- https://www.shuxuele.com/data/probability-events-types.html
- https://www.zhihu.com/question/264373830/answer/613608291
- https://blog.csdn.net/u013371163/article/details/60469065
- https://zhuanlan.zhihu.com/p/78297343